Вейвлет своими руками
В предыдущей
статье мы сформулировали краткое определение вейвлет-анализа и описали
некоторые области его применения. Теперь настало время дать простой
рецепт, на основании которого каждый может построить целое семейство
вейвлетов 'в домашних условиях' и оценить достоинства вейвлет-анализа,
применив их к имеющимся данным. Этот способ построения вейвлетов был
предложен американским математиком И.Добеши в ее работе [1].
Дадим вначале определения некоторых терминов, которыми будем
оперировать в дальнейшем. Любую упорядоченную последовательность данных,
заданную аналитически (в виде некоторой функции) или перечислением ее
значений будем называть сигналом. Значение сигнала может зависеть
от одного параметра (например, от времени) или от нескольких. Например,
фотографическое изображение можно считать двумерным сигналом, значением
которого является яркость каждой точки изображения, а параметрами –
координаты точки по горизонтали и по вертикали. При цифровой обработке
сигнала над ним обычно выполняют некоторое преобразование,
выявляющее характерные особенности данного сигнала и, выполнив
определенные действия (например, подавление шума), делают обратное
преобразование. Классическим примером является преобразование Фурье,
переводящее сигнал из временной области в частотную и обратно.
Преобразование, как прямое, так и обратное, расчитывается путем вычисления
свертки сигнала в каждой его точке с некоторой функцией, называемой
фильтром. В дискретном случае фильтры задаются просто перечислением
их значений (коэффициентов) в точках дискретизации. Учитывая
статистические особенности большинства сигналов (полезная информация
расположена в низкочастотной области спектра сигнала, а помехи или
шум – в высокочастотной), сигнал обычно преобразуют с использованием
двух дополняющих друг друга фильтров – низких и высоких частот.
Вейвлеты, описываемые нами, относятся к классу квадратурных зеркальных
фильтров (КЗФ). Особенностью этого класса фильтров является то, что
фильтр высоких частот получается из соответствующего фильтра низких частот
простой перестановкой его коэффициентов в обратном порядке и изменением
знака половины из них (только четных или только нечетных). При этом
вейвлет выделяет локальные особенности сигнала в каждой точке и является,
таким образом, фильтром высоких частот, а соответствующий фильтр низких
частот описывается так называемой масштабирующей функцией.
Пусть, например, фильтр имеет носитель длиной 4 (т.е. описывается
четырьмя коэффициентами в дискретном случае). Представим сигнал в виде
вектора длиной N, где N – количество отсчетов. Тогда процесс
преобразования сигнала можно записать в матричном виде:
| C0 |
C1 |
C2 |
C3 |
0 |
0 |
… |
0 |
0 |
0 |
0 |
|
F0 |
| 0 |
C0 |
C1 |
C2 |
C3 |
0 |
… |
0 |
0 |
0 |
0 |
|
F1 |
| 0 |
0 |
C0 |
C1 |
C2 |
C3 |
… |
0 |
0 |
0 |
0 |
|
F2 |
| 0 |
0 |
0 |
C0 |
C1 |
C2 |
… |
0 |
0 |
0 |
0 |
|
F3 |
| … |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
x |
… |
| 0 |
0 |
0 |
0 |
0 |
0 |
… |
C0 |
C1 |
C2 |
C3 |
|
Fn-3 |
| C3 |
0 |
0 |
0 |
0 |
0 |
… |
0 |
C0 |
C1 |
C2 |
|
Fn-2 |
| C2 |
C3 |
0 |
0 |
0 |
0 |
… |
0 |
0 |
C0 |
C1 |
|
Fn-1 |
| C1 |
C2 |
C3 |
0 |
0 |
0 |
… |
0 |
0 |
0 |
C0 |
|
Fn |
Здесь C0…C3 означают коэффициенты фильтра длиной
4, F0…Fn – значения отсчетов сигнала, символ
x – операция умножения матрицы на вектор. Обратите внимание на четыре
последние строки матицы – такой 'заворот' фильтра означает, что мы
продолжаем наш сигнал на всю числовую прямую периодическим образом (т.е.
считаем, что после значения Fn снова идет значение
F0). В результате умножения матрицы размерностью NxN на вектор
длиной N мы получаем вектор такой же длины, а с учетом того, что в
преобразовании участвуют два фильтра, даже два вектора длины N вместо
одного – казалось бы, никакого выигрыша мы не получили. Однако
вейвлеты Добеши обладают следующим свойством: как сглаженное представление
сигнала (т.е. обработанное масштабирующей функцией), так и его локальные
особенности (полученные в результате вейвлет-преобразования) обладают
избыточностью в два раза. Другими словами, для вейвлета длиной 2N
результат преобразования сигнала в каждой точке представляет собой
некоторое 'усреднение' сигнала и набор 'деталей', отличающих исходный
сигнал от усредненного – причем усредненный сигнал является в 2 раза
'более гладким', чем исходный. Таким образом, каждый четный или каждый
нечетный отсчет преобразования может быть исключен из рассмотрения, и в
результате преобразования мы получим два вектора вдвое меньшей длины, один
из которых содержит сглаженную версию сигнала (или представление сигнала в
половинном масштабе), а другой – набор локальных особенностей (то
есть помехи на данном уровне детализации)! Что это дает? Во-первых, анализ
сглаженного сигнала упрощает выявление его характерных свойств (например,
нейросети гораздо лучше обучаются на сигналах, очищенных от шума, чем на
зашумленных). Во-вторых, анализ локальных особенностей сигнала позволяет
не только определить характер и параметры помех, но и четко локализовать
'особые точки' сигнала – такие как выбросы, пропущенные значения,
резкие скачки уровня и т.д. Более того, если полученный сигнал все еще
недостаточно очищен от помех, мы можем повторно применить к нему
вейвлет-преобразование и получить еще более гладкую версию сигнала (уже в
четыре раза короче, чем исходный) и локальные особенности сигнала уже на
следующем уровне детализации!
С учетом сказанного, мы можем выполнять преобразование сигнала не в
каждой его точке, а только в тех, которые будут участвовать в дальнейшем
рассмотрении, то есть только в четных или только в нечетных. Заметим, эта
фраза означает только то, что свертка вычисляется в половине точек, но в
вычислении участвуют все M последовательных точек, где M –
длина фильтра. Тогда матрица преобразования будет иметь размерность
(N/2)xN (N – четное) и примет следующий вид (не забыв при этом, что
имеем две матрицы – одну для масштабирующей функции, другую –
для вейвлета):
| C0 |
C1 |
C2 |
C3 |
0 |
0 |
… |
0 |
0 |
0 |
0 |
|
F0 |
| 0 |
0 |
C0 |
C1 |
C2 |
C3 |
… |
0 |
0 |
0 |
0 |
|
F1 |
| 0 |
0 |
0 |
0 |
C0 |
C1 |
… |
0 |
0 |
0 |
0 |
|
F2 |
| 0 |
0 |
0 |
0 |
0 |
0 |
… |
0 |
0 |
0 |
0 |
|
F3 |
| … |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
x |
… |
| 0 |
0 |
0 |
0 |
0 |
0 |
… |
0 |
0 |
0 |
0 |
|
Fn-3 |
| 0 |
0 |
0 |
0 |
0 |
0 |
… |
C2 |
C3 |
0 |
0 |
|
Fn-2 |
| 0 |
0 |
0 |
0 |
0 |
0 |
… |
C0 |
C1 |
C2 |
C3 |
|
Fn-1 |
| C2 |
C3 |
0 |
0 |
0 |
0 |
… |
0 |
0 |
C0 |
C1 |
|
Fn |
| C3 |
-C2 |
C1 |
-C0 |
0 |
0 |
… |
0 |
0 |
0 |
0 |
|
F0 |
| 0 |
0 |
C3 |
-C2 |
C1 |
-C0 |
… |
0 |
0 |
0 |
0 |
|
F1 |
| 0 |
0 |
0 |
0 |
C3 |
-C2 |
… |
0 |
0 |
0 |
0 |
|
F2 |
| 0 |
0 |
0 |
0 |
0 |
0 |
… |
0 |
0 |
0 |
0 |
|
F3 |
| … |
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
x |
… |
| 0 |
0 |
0 |
0 |
0 |
0 |
… |
0 |
0 |
0 |
0 |
|
Fn-3 |
| 0 |
0 |
0 |
0 |
0 |
0 |
… |
C1 |
-C0 |
0 |
0 |
|
Fn-2 |
| 0 |
0 |
0 |
0 |
0 |
0 |
… |
C3 |
-C2 |
C1 |
-C0 |
|
Fn-1 |
| C1 |
-C0 |
0 |
0 |
0 |
0 |
… |
0 |
0 |
C3 |
-C2 |
|
Fn |
Хорошо, принцип вейвлет-преобразования сигнала уже понятен. Но как
найти значения коэффициентов, составляющих матрицу? Для этого можно
использовать следующие свойства вейвлетов Добеши:
- Сдвиги вейвлета образуют ортонормированный базис пространства, т.е.
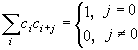 Другими словами, при попарном
перемножении строк матрицы преобразования, мы должны получить 0, а при
умножении строки на саму себя – 1. Свойство ортогонормированности
базиса означает, что матрица обратного преобразования представляет собой
просто транспонированную матрицу прямого преобразования.
Другими словами, при попарном
перемножении строк матрицы преобразования, мы должны получить 0, а при
умножении строки на саму себя – 1. Свойство ортогонормированности
базиса означает, что матрица обратного преобразования представляет собой
просто транспонированную матрицу прямого преобразования.
- Вейвлет длиной M (M – четное) имеет M/2 нулевых начальных
моментов, т.е.
 . Поскольку начальные моменты
вейвлета инвариантны относительно сдвига вдоль его области определения,
мы можем взять произвольные последовательные значения xi –
например, 0, 1, 2 … M. Количество нулевых моментов вейвлета означает,
что если аппроксимировать исходный сигнал полиномиальными сплайнами
степени M, то вейвлет-преобразование 'погасит' все полиномиальные
составляющие степени от 0 до M/2 (т.е. вейвлет-преобразование полинома
определенной 'гладкости' будет давать нулевой отклик).
. Поскольку начальные моменты
вейвлета инвариантны относительно сдвига вдоль его области определения,
мы можем взять произвольные последовательные значения xi –
например, 0, 1, 2 … M. Количество нулевых моментов вейвлета означает,
что если аппроксимировать исходный сигнал полиномиальными сплайнами
степени M, то вейвлет-преобразование 'погасит' все полиномиальные
составляющие степени от 0 до M/2 (т.е. вейвлет-преобразование полинома
определенной 'гладкости' будет давать нулевой отклик).
Таким образом, для нахождения значений коэффициентов вейвлет-фильтра
длиной 4, мы должны решить систему из 4 алгебраических уравнений:

Решением этой системы являются следующие значения:
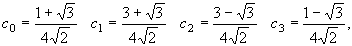
или
С0
= 0.4829629131445341
С1
= 0.8365163037378097
C2
= 0.2241438680420134
C3
= –0.1294095225512604
Соответственно, в случае вейвлета Добеши длиной 6 (3 нулевых момента)
мы будем иметь 6 коэффициентов и 6 уравнений для их нахождения: 3
уравнения, вытекающих из условия ортогональности, и 3 уравнения нулевых
моментов. Решение такой системы может быть представлено в виде:
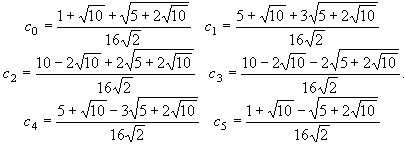
Для выполнения обратного преобразования достаточно вычислить
произведение транспонированных матриц коэффициентов на 'сглаженный' вектор
и вектор 'деталей' соответственно и выполнить покомпонентное сложение
результатов. Заметим, что сдвиг коэффициентов в матрице на 2 означает в
этом случае вставку нулей между отсчетами, при этом вектор длины N/2
дополняется до длины N исходного вектора.
В заключение статьи дадим несколько советов по усовершенствованию
нашего алгоритма, называемого алгоритмом Малла (Mallat algorithm).
- Известно, что свертке функций во временной области соответствует
умножение их изображений в частотной области. Если сигнал представлен
достаточно большой выборкой, то более эффективным методом выполнения
преобразования является вычисление преобразования Фурье сигнала и
фильтра, покомпонентное перемножение соответствующих векторов,
вычисление обратного преобразования Фурье результата (при этом получаем
избыточное представление) и 'прореживание' преобразованного сигнала
нужным образом (удаление всех четных или нечетных отсчетов).
- Для вычисления вейвлет-преобразования двумерного сигнала (например,
изображения), представленного прямоугольной матрицей отсчетов, нужно
вначале выполнить преобразование над каждой строкой исходной матрицы, а
затем над каждым столбцом полученного результата (или наоборот). В
результате мы получим уже 4 матрицы, каждая высотой и шириной вдвое
меньше исходной, соответствующих 'сглаженному' изображению и наборам
деталей по горизонтали, по вертикали и по диагонали соответственно.
Аналогичным образом может быть выполнено и преобразование сигналов
больших размерностей.
Андрей Киселев
BaseGroup Labs
Список литературы:
- Добеши, И. Десять лекций по вейвлетам. М., РХД, 2001.
- Vaidyanathan, P.P. Proceedings of the IEEE, 1990, vol. 78, pp.
56-93
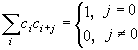 Другими словами, при попарном
перемножении строк матрицы преобразования, мы должны получить 0, а при
умножении строки на саму себя – 1. Свойство ортогонормированности
базиса означает, что матрица обратного преобразования представляет собой
просто транспонированную матрицу прямого преобразования.
Другими словами, при попарном
перемножении строк матрицы преобразования, мы должны получить 0, а при
умножении строки на саму себя – 1. Свойство ортогонормированности
базиса означает, что матрица обратного преобразования представляет собой
просто транспонированную матрицу прямого преобразования.